- UID
- 745548
- 在线时间
- 小时
- 注册时间
- 2012-4-5
- 最后登录
- 1970-1-1
- 主题
- 帖子
- 性别
- 保密
|
Speed1
The demographic transition
More or less
Go forth and multiply
 ONE of the most significant phenomena of modern history is the demographic transition: as people get richer, they have smaller families. This slowing of reproduction with economic development is the reason why Thomas Malthus’s prediction of disaster, caused by the human population outstripping its supply of food, is unlikely ever to come true. In the short term, Malthusian doom has been evaded by innovations that increased the food supply. But in the long term it is likely to be a ceiling on demand that helps to save humanity. The world’s population, now some 7 billion, is expected to level out at a little over 10 billion towards the end of the century. ONE of the most significant phenomena of modern history is the demographic transition: as people get richer, they have smaller families. This slowing of reproduction with economic development is the reason why Thomas Malthus’s prediction of disaster, caused by the human population outstripping its supply of food, is unlikely ever to come true. In the short term, Malthusian doom has been evaded by innovations that increased the food supply. But in the long term it is likely to be a ceiling on demand that helps to save humanity. The world’s population, now some 7 billion, is expected to level out at a little over 10 billion towards the end of the century.
Why the demographic transition happens, though, is obscure—for this reaction by Homo sapiens to abundance looks biologically bonkers. Other species, when their circumstances improve, react by raising their reproductive rate, not curtailing it. And work just published by Anna Goodman of the London School of Hygiene and Tropical Medicine and her colleagues, in the Proceedings of the Royal Society, suggests what humans do is indeed bananas. Dr Goodman has shown that the leading explanation advanced by biologists for the transition does not, in the context of the modern world, actually deliver the goods.
This explanation is that, according to circumstances, people switch between two reproductive strategies. One, known to ecologists as “r-selection”, is to produce lots of offspring but invest little in each of them. This works in environments with high infant mortality. The other, known as “K-selection”, is to have only a few offspring but to nurture them so that they are superb specimens and will thus do well in the competition for resources and mates, and produce more grandchildren for their parents than their less well-nurtured contemporaries. The demographic transition, according to this analysis, is a shift from r-type to K-type behaviour.
[308]
Speed2
To test this idea, Dr Goodman turned to Sweden—specifically, to a group known as the Uppsala Birth Cohort. These people (there are about 14,000 of them) were born between 1915 and 1929 in Uppsala University Hospital. They and their descendants have subsequently been tracked by Sweden’s efficient system of official records. Among other things these records show their income and socioeconomic status (which, crucially, are also known for the parents of members of the original cohort), how many children have been born to cohort members and their descendants, and when. These data were Dr Goodman’s raw material.
If the r/K interpretation is correct (the letters stand for the rate of reproduction and the “carrying capacity”, or resource richness, of the environment), then an advantage of some sort for the socioeconomically privileged should show up as the generations succeed one another. Dr Goodman’s analysis shows that it does, but in a way that is not translated into any obvious evolutionary advantage.
Reducing family size certainly creates what look, on the face of things, like more competitive descendants. Children, grandchildren and great-grandchildren alike get better marks at school, are more likely to go to university and have higher incomes as adults. What these competitive individuals do not do, though, is go on to compete in the one arena which matters in a Darwinian sense: reproduction. If anything, the tendency towards smaller, more socially successful families tends to feed back on itself over the generations, and the contribution of the K-selected to the gene pool therefore shrinks.
[255]
Speed3
To biologists, this is all very puzzling. If K-type behaviour is not delivering the goods then it should never have come about in the first place. But there may be an explanation: that the psychological make-up which encourages K-type behaviour worked in the past but is not appropriate to modern circumstances.
This does seem plausible. In large parts of the world, better hygiene, nutrition and medicine have almost abolished child mortality, meaning the advantage of K over r is diminished. Education is available free to all. And harem-formation, which would have been an option in the past for many K-selected males, is frowned on these days. In other words, the disadvantages of being r-selected have disappeared.
The upshot is that the demographic transition may be the result of a mismatch between ancient psychology and the modern world. In that, it would be like the epidemic of obesity which results from stone-age appetites meeting capitalist abundance. Unlike obesity, though, small families do no harm to the individuals involved. In fact this particular mismatch may actually be all that stands between humanity and ecological disaster.
New carnivorous harp sponge discovered in deep sea
A blog by Scientific American.
You may remember the Monterey Bay Aquarium Research Institute (MBARI) from such discoveries as the Yeti crab, the squid with elbows and my personal favourite, the pigbutt worm, and now they’re back with footage of a new species of carnivorous sponge.
Seventeen years ago, Jean Vacelet and Nicole Boury-Esnault from the Centre of Oceanology at France’s Aix-Marseille University provided the first real evidence that a sponge could be more than, well, a sponge. They had discovered a new species of deep-sea sponge living in the unusual setting of a shallow Mediterranean sea cave, the inside of which mimicked the conditions of its usual habitat more than a kilometre below the surface. This allowed the researchers an unprecedented view of the sponge’s eating habits, and they watched as it snared its prey of small fish and crustaceans instead of absorbing bacteria and organic particles through their bodies, like most other sponge species do – including ones living in the very same cave.
[357]
Speed4
Vacelet and Boury-Esnault’s sponges were of the Asbestopluma genus and belonged to the Cladorhizidae family of carnivorous demosponges – the class that contains over 90% of the world’s sponges. Since reporting their discovery in a 1995 issue of Nature, 24 new species of cladorhizid sponges, including the incredible ping-pong tree sponge (see below), have also been discovered. Yet due to the difficulty of studying their behaviour at such incredible depths, researchers have had little opportunity to describe essential aspects of their lives, particularly how they reproduce.

Chondrocladia, or ping-pong, sponge.MBARI
Which is where MBARI’s remotely operated vehicles (ROVs) Tiburon and Doc Ricketts, come in. Using these deep-diving vessels, a team of researchers led by Senior Research Technician Lonny Lundsten discovered a species of harp sponge called Chondrocladia lyra off the coast of California, at depths of 3316–3399m.
As Mr_Skeleton pointed out on Reddit this week, this sponge doesn’t look like it could clean anything. But it can catch prey, envelope it in membrane and digest it whole, so it certainly has other priorities. Based on footage of several individuals and two large, fragmentary specimens brought up by the ROVs, Lundsten’s team described how the vertical branches and horizontal stolons that make up the sponge’s basic harp-like structure, called a vane, are covered in barbed hooks and spines. They found that a number of crustacean prey were passively ensnared on these branches thanks to the Velcro-like hooks and then aggressively enclosed in a cavity to be dismembered into small, digestible particles, which provided direct evidence of the species’ carnivorous appetites.
[260]
Speed5
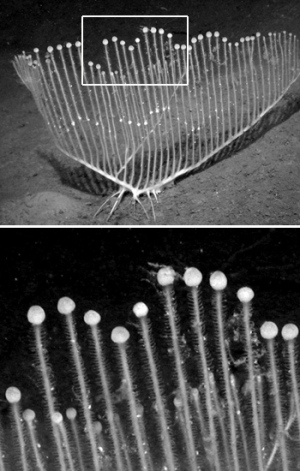
The vertical branches of the harp sponge are tipped by swollen terminal balls containing packets of sperm.MBARI
C. lyra can grow up to 37cm long – impressive for a sponge – and are anchored to the sea-floor by a structure called a rhizoid, which looks like a root system. They can have 1-6 vanes, each supporting a number of equidistant vertical branches, and each of these end in swollen terminal balls. According to the researchers, these terminal balls produce condensed packets of sperm called spermatophores, which are released into the surrounding water in the hopes of fertilising other harp sponges in the area. Each C lyra sponge also has an egg development area around the mid-point of the branches, and when the spermatophores make contact, these areas swell up as the eggs are fertilised and begin to mature.
The team suggests that the structure of the harp sponge is designed to ensure that they catch the most prey possible, and also maximise their chances of catching spermatophores from other harp sponges.
“Video footage taken as the ROVs approached specimens of C. lyra provided information about the biological diversity of the areas in which the sponges live,” the researchers added in their report in the current issue of Invertebrate Biology. “Among the coexisting invertebrates were unidentified sea anemones; the soft coral Anthomastus robustus, members of several species of sea pens; and the sea cucumber Paelopadites confundens, as well as another sea cucumber in the family Elipidiidae.”
[226]
越障
3-D printing enters the fourth dimension
An article by Scientific American.
I was at a math conference last week, and one of the other attendees brought a puzzle. I am a pretty slow puzzle-solver, so it will be a while before I figure out how to assemble those five pieces to get this.

Saul Schleimer and Henry Segerman
Saul Schleimer, a mathematician at the University of Warwick who was at the conference with me, and Henry Segerman, a mathematician at the University of Melbourne, are the co-creators of the Thirty Cell puzzle. They are both theoretical math researchers who also enjoy using 3-D printing—a technique for manufacturing a three-dimensional object from a computer program—to create mathematical art and visualizations. (In August, Scientific American featured some of Segerman’s sculptures in a slide show from the Bridges math-art conference.)
 Three views of the assembled puzzle.Saul Schleimer and Henry Segerman Three views of the assembled puzzle.Saul Schleimer and Henry Segerman
This puzzle is a projection of a four-dimensional shape into our three-dimensional world. To explain how the projection was created, Schleimer brings it down a dimension and starts with a three-dimensional cube. Imagine a cube sitting inside a sphere. Now put yourself at the middle, holding a flashlight. The light projects all the edges and vertices out to the surface of the sphere. “We replace the usual cube that we know and love with a roundy cube on the sphere,” says Schleimer. This process is called radial projection.
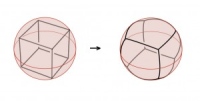
Left: a cube inside a sphere. Right: radial projection from the center of the cube onto the surface of the sphere.
Saul Schleimer and Henry Segerman
From there, a process called stereographic projection places the “roundy cube” onto a flat two-dimensional plane. To visualize this, imagine that the sphere has a plane running through its equator. A line connecting the north pole of the sphere to a point of the cube on the sphere’s surface then intersects the equatorial plane at one point.
The collection of all those intersection points is the stereographic projection of the cube. (In general, stereographic projection can be defined for many different planes through the sphere, but the equatorial plane is the one used in this case.)

Left: Stereographic projection from the circle to the line. Right: Stereographic projection from the sphere to the plane.
Saul Schleimer and Henry Segerman
For the puzzle Segerman and Schleimer created, the whole process goes up a dimension. The accompanying informational sheet describes it succinctly: “When assembled the 30-cell puzzle is a part of the stereographic projection of the radial projection of the 120-cell in four-space to the three-sphere to three-space.”
The 120-cell is one of the six convex, regular polytopes in four dimensions. These are the four-dimensional equivalents of the regular polygons (such as the equilateral triangle and square) and Platonic solids, a class of three-dimensional figures. Schleimer says that dimension four is ideal for interesting regular polytopes because it has enough examples to be interesting, but not too many. In two dimensions, there are infinitely many regular polygons, and in five and higher dimensions, there are only three different kinds of regular polytopes. There are five three-dimensional Platonic solids, and dimension four has six regular polytopes. The 120-cell is one of those six. It is made of 120 dodecahedral cells, with four meeting at each vertex.

Stereographic projection of the "roundy cube" to the two-dimensional plane.
Saul Schleimer and Henry Segerman
Schleimer says that he and Segerman started working on this model when they were studying a topological object called the Hopf fibration. The 120-cell arose naturally in their work, and they decided that they wanted to try to visualize it as an actual three-dimensional object, not just a computer representation or theoretical object in their minds. After creating the first printed model on a 3D printer, Schleimer and Segerman discovered new aspects of the shape. “In a way, producing the 3-D model helped us find some cool stuff that we didn’t realize was there. We understood it somewhat, and we produced this awesome toy, and we’ve learned new math,” says Schleimer.
Segerman’s and Schleimer’s first experiments with the 120-cell led to a few different 3-D models. Creating a projection of the whole 120-cell was prohibitively expensive, so they have been experimenting with different subsets of the object. ”We’re having a good time finding chunks to stereographically project,” says Schleimer. One of the models was this set of three rings, which he calls a “fidget.”

Saul Schleimer and Henry Segerma
It’s not a puzzle, but it’s fun to play with, and there are several interesting configurations for it. Segerman demonstrates them and explains a little more in the video at the top of the page.
As Segerman says, the fidget led him and Schleimer to develop the puzzle version of the 120-cell, which I now get to play with.
3-D printing is not new, but it is getting more popular, and the number of media—metals, plastics, sugar, and so on—that can be used as “ink” is growing. It is being used for creating engineering prototypes, model skulls for paleontology research and even artificial blood vessels. Segerman wrote an article for the Mathematical Intelligencer about using 3-D printing in math
Segerman and Schleimer use the company Shapeways to print their models. They use programs such as Python, Adobe Illustrator and Rhino to create files of an object that they send to Shapeways to translate into very precise 3-D models. Shapeways uses the computer files to program a laser to fuse powders into the shape of a 3-D object. It can even print objects with multiple interlinked components, such as the the fidget above. Another popular type of 3D printer, MakerBot, melts new layers of a material over previously deposited ones, so the models must be supported during the entire process. Shapeways doesn’t have that constraint, but its printers are more expensive. The company lets people upload their models and then ships the printed material out to them, rather than having users own printers themselves.
The puzzle Schleimer sold me is made of tough but slightly flexible nylon. He and Segerman also printed a larger one in bronze for a friend, but unfortunately no one has been able to put it together yet.“The math is fine, but the physics isn’t fine,” says Schleimer. The plastic models have an almost imperceptible amount of flex in them, but the bronze is too rigid.
[1062]
|
|

 京公网安备11010202008513号 京ICP证101109号 京ICP备12012021号
京公网安备11010202008513号 京ICP证101109号 京ICP备12012021号